As decision makers, we’d like to think that the more we understand what statistics and analytics do for us, the easier our lives become. Unfortunately (and just like with statistics), it’s not that simple.
The main reason for this difficulty lies in what we understand the purpose of statistics and analytics to be. Coaches, being casual consumers of statistics and analytics, tend to think that data offers them certainty, a clear path from the darkness to the light. Professional statisticians and decision scientists tell a different story. They use “certainty” differently than coaches do - they use it to describe a spectrum rather than a binary. To them, an event is not either certain to happen or not, instead they think of how certain (or how likely) an event is to happen. This, to oversimplify, is probability.
In volleyball, a clear example of this can be found in the serve-pass battle. Coaches will often choose a serving target based on reception averages. They will try to serve a passer who averages 2.0 instead of one who averages 2.4. The main difference between coaches and statisticians is what each thinks will happen when the ball is passed. The coach tends to be certain the pass from the weaker passer will be, at best, a 2 while the statistician tends to think about how certain (how probable) each different reception outcome is. (Here’s a journal article that describes a very similar point to the one I’m making here.) The coach is correct that the passer puts up a 2 on average but that is a bit too imprecise for the statistician. The statistician will think in terms of how frequently a 2-option pass actually happens compared to other reception grades. (To get a little more nerdy, statisticians will refer to the mode, or which outcome is most common.)
The point of this comparison is not to rehash how averages are calculated or even how coaches use them. The point isn’t even to demand changes to the decisions a coach makes. (You should probably serve the 2.0 passer and not the 2.4 passer if you’re trying to get your opponent out of system.) I want coaches to think more about how constantly using averages influences our thinking. Averages have a way of allowing us to forget the underlying variability that create them and this can have consequences for how we treat coaching decisions. To remind me of this variability, I think of a volleyball match as twelve slot machines running around in shorts.
When I pull the arm of a slot machine, I acknowledge that I don’t know what the outcome will be, I only know what I want it to be. Knowing a slot machine’s average pay out does not guarantee that it actually will pay out on any given pull. My home state of Colorado has legal gambling in a few areas and the statewide data shows that slot machines pay out an average of 91.9% of what is put in. No one expects to put a dollar coin into a slot machine and receive 91.9 cents back but that’s what coaches do when they expect a 2.0-average passer to pass a 2 every time they are served. There’s a big difference between averaging a 2.0 in passing and passing a 2 every time.
When coaches select strategies or make other decisions, they aren’t choosing the outcomes, they are actually choosing which slot machine to pull. The role of statistics and analytics is to inform coaches so that they can hedge their bets. To go back to Colorado slots, penny slots pay out an average of 90.4% but dollar slots pay out an average of 93.8% so a player will lose a smaller percentage on average playing dollar slots. But when a player armed with that knowledge chooses to play a particular dollar slot instead of a particular penny slot, knowing that statistic doesn’t guarantee that the machine will pay out when they play it. Knowing the probability for a given situation allows the player to select a strategy that, hopefully, maximizes the likelihood of a favorable outcome but that outcome is far from guaranteed.
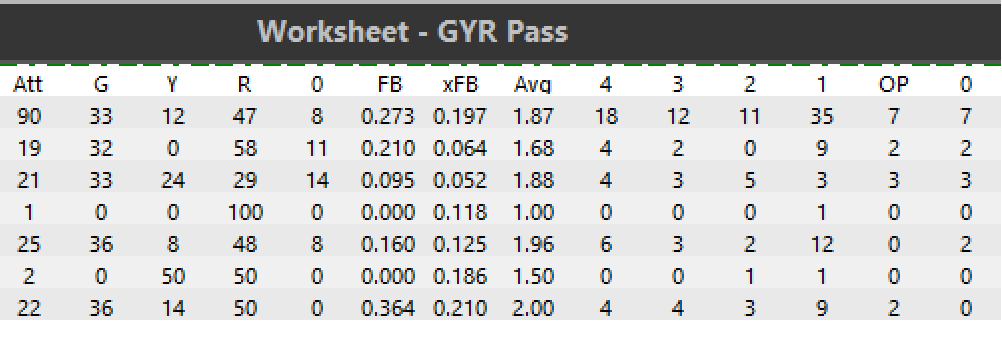
Let’s go back to the decision between serving targets. The point isn’t to talk you into serving the 2.4 passer, it’s to get you to think differently about what happens when the 2.0 passer receives the ball. I’ll show you what I mean. Here’s a worksheet I use in competition that shows a tough day at the office for serve receive for one match.
The G, Y, R, and 0 columns are percentages while the 4, 3, 2, 1, OP, and 0 columns are counts. I don’t need to explain a lot more about how this sheet works for you to see that, even when the entire team passes below 2.0, 1/3 of the receptions are actually in system or pretty close to perfect (4s and 3s). 1/3 of the time feels like a lot when a team passes 1.9 but that’s the point I’m making. As an analyst, I’m not surprised when a pass is perfect because I know that those outcomes happen fairly often, just not as often as 1s (nearly 1/2 the time in this match). The message is that the server probably didn’t do anything wrong when someone passes their serve perfectly, even if that someone is passing 2.0 or worse. In this match, an in-system pass is the second-most likely outcome after all. Recognizing such variability can help coaches stay open when the outcomes aren’t what they hoped for. If coaches steer clear of expecting certain outcomes, they are less likely to think of outcomes as wrong or bad. I am encouraging coaches to think of those bad outcomes as less likely or maybe even unlucky.
If you shift your thinking to embrace the fact that bad outcomes are still part of a good performance, then you can shape your judgement and your feedback accordingly. You can judge your decision and the player that carries it out based on the process you used to make the decision rather than on the outcome the decision yielded. Averages are an accumulation of single actions so, if your decision-making process is sound, you don’t lose faith in the individual choices you make and, more importantly, you don’t lose faith in the players. Just as you trust your decisions, you trust that the players are doing their best to execute, even if sometimes the outcomes don’t show it.